Om universet for viderekommende - del 4

Antall rotasjoner - gåten løst?

Av Sverre Avnskog

Frem til nå har det vært en akseptert sannhet at det ikke står opplyst i VmL det nøyaktige antall ganger modersolparene roterer på sin veg rundt sentralsolen. Jeg har også tilhørt dem som har vært av denne oppfatningen. Men når man forsker tilstrekkelig lenge nok i en tekst som den om universet i VmL, så hender det at man når så dypt inn i teksten, at svaret likevel plutselig åpenbarer seg - man har bare ikke klart å se det tidligere. Og ofte er det det mest selvfølgelige som er det vanskeligste å se. Personlig har jeg syslet med å forsøke å forstå denne teksten nærmest daglig i mer enn fire år, og utallige er de skissene jeg har tegnet og beregninger jeg har foretatt. Jeg har i andre artikler påvist hvorfor den såkalte planmodellen ikke tilfredsstiller VmLs beskrivelse, og hvorfor det kun er helixmodellen som gjengir korrekt den beskrivelsen som gis i VmL. Jeg vil i denne artikkelen gi det korrekte svaret på hvor mange ganger modersolene roterer i løpet av et løp rundt sentralsolen. Jeg vil også presentere en animasjon som viser alt dette, og selvfølgelig vil jeg forklare hvilke avsnitt fra VmL det er som gjør at jeg er så sikker på å ha funnet det rette svaret.

(se animasjonen i fullskjerm - åpnes i nytt vindu)

Her er en del av den teksten i VmL, der det forklares hvordan modersolparene beveger seg rundt sentralsolen:

"Afstanden mellem de parvis stillede Modersole, regnet fra hver Sols Centrum, er = Radius i Centralsolen (Guds Rige). Parrenes fælles Bane[1] om Centralsolen beskriver en fuldkommen Cirkel, hvis Radius er = 7 Gange Radius i Centralsolen. Denne Storcirkels Periferi skærer Centrum i Afstandsrummet mellem de parvis stillede Modersole; derved falder Modersolenes Særbevægelse halvvejs udenfor, halvvejs indenfor Storcirklens Periferi[2].
    Modersolene afbalancerer hinanden Par og Par ved lige Tiltrækning og lige Frastødning. Den engang givne Afstand vil saaledes bestandig bibeholdes.
    De parvis stillede Soles Særbevægelse efter hinanden omkring Centralsolen udføres i et aabent Cirkelløb (Spiralløb)[3],saa at Centrum i hvert Pars Afstandsrum glider frem ad Storcirklens Periferi.
    Parrene har en hinanden modgaaende Bevægelse[4].
    Har man paa Papiret nedfældet et Billede med Moderparret a-b staaende til venstre for Centralsolen og Parret c-d til højre, alle fem Sole i Opposition til hverandre og saaledes at a og c staar nærmest Centralsolen, b og d fjernest, har - naar man tænker sig denne Stilling som Udgangspunkt for Modersolenes Bevægelse - Solene a og c begge en fra Centralsolen bortgaaende Bevægelse, b og d en mod Centralsolen sig nærmende Bevægelse. Parret a-b's Spiralløb[5] gaar saaledes fra venstre Side af Centralsolen om til højre, Parret c-d's fra højre Side om til venstre. Efter ca. 3 Millioner Aar vil Parret a-b have indtaget Parret c-d's Stilling til højre for Centralsolen og Parret c-d vice versa[6]. Hele Omløbstiden for begge Parrene, ad den fælles Bane om Centralsolen, er = 2 Tidsevigheder, der svarer til ca. 6 Millioner Aar.
    Den engang givne Rotationshastighed for begge Parrene vil bestandig bibeholdes, idet de, paa hvert givet Tidspunkt, alle udøver en gensidig Afbalancering, saa at Parrenes Ligevægtsstilling, med Guds Rige som Centralsol, ingen Sinde forrykkes."

Som man ser, har jeg merket en del viktige begreper og avsnitt i teksten, og jeg vil her gå gjennom dem ett for ett, og vise hvorfor jeg mener animasjonene som kan ses ovenfor, er de eneste bevegelsene som tilfredsstiller forklaringen i VmL fullt ut.

[1]: Parrenes fælles bane. Ser man på den øverste animasjonen, som viser helixmodellen sett rett ovenfra, vil man se, at når begge parene har nådd halvveis rundt sentralsolen, når de frem til de røde sporene som det andre parets bane har tegnet opp. Man vil se at hvert par glir fullkomment inn i de sporene som det andre paret har etterlatt seg, og dette viser med all mulig tydelighet at de to parene har en felles bane rundt sentralsolen. Dette er ikke tilfelle for planmodellens vedkommende. Der har hver modersol hver sin bane, og det dannes altså 4 spor. Planmodellen tilfredsstiller ikke VmLs forklaring på dette punktet!

Slik ser sporene ut i Jørgen Degns animasjon av planmodellen. Parene har på dette stillbildet beveget seg litt over halvveis rundt sentralsolen, og man ser tydelig hvordan det røde og hvite sporet (a-b) ikke faller sammen med det grønne og gule (c-d) - det dannes tvertimot fire spor. Man kan demed ikke si at modersolparene har en felles bane rundt sentralsolen!

[2]: Modersolenes Særbevægelse (falder) halvvejs udenfor, halvvejs indenfor Storcirklens Periferi. Igjen henviser jeg til den øverste animasjonen, der modersolparenes spor vises ovenfra. Fordi modersolparene rotasjonsplan står vinkelrett på storsirkelens plan, vil ikke den situasjonen oppstå at de to parene får helt ulike sporlengder. Begge parenes spor vil være fullkomment identiske. Ut fra animasjonene over, er det meget vanskelig å danne seg en sikker oppfatning av den enkelte modersols hastighet, men med det blotte øye ser det ut som hastigheten for alle modersolenes vedkommende ser meget jevn ut, uten noen store akselerasjoner, slik som det vil være i planmodellen. For de røde sporenes tilfelle, kan det se ut som yttersporene er noe lengre, men her må vi huske på at sporene må oppfattes i 3 dimensjoner, og det vil derfor være ytterst vanskelig å beregne den nøyaktige lengden. For planmodellens vedkommende fremgår det av tallene i artikkelen "Om universet for viderekommende - del 3" at den prosentvise fordelingen aldri noensinne, uansett antall rotasjoner vil kunne bli 50/50. Den minste prosentvise forskjellen finner man ved de høyeste verdiene, men forskjellen vil aldri kunne bli mindre enn ca 2,3%. Den største forskjellen er opp mot 6% - og det er vel og merke forskjeller som er regnet ut på en meget "snill" måte - ved at man legger sammen begge modersolparenes verdier utenfor og innenfor storsirkelens periferi, og deretter regner ut forskjellen. Dersom man undersøker forskjellen for hvert par for seg, vil man f. eks. ved N=14 se at fordelingen utenfor/innenfor er ca 72/28 for modersolpar c-d og ca 31/69 for a-b. Regner man ut en gjennomsnittlig forskjell for de to parenes vedkommende ved verdien N=8, vil man finne at den er mer enn 41%! Hvordan kan dette rime med VmLs ord om at bevegelsen skal foregå halvveise utenfor og halvveis innenfor storsirkelens periferi?

Slik ser et stillbilde av helixmodellens modersolspor ut - sett rett ovenfra. Bildet er tatt rett før modersolparene har fullført en rotasjon rundt sentralsolen - med to innbyrdes rotasjoner i hvert par. Som man ser, vil alltid modersolparenes bevegelser danne fullkomne speilbilder av hverandre, både hva angår hastighet og posisjon. Modersolene vil bytte på å ha yttersving og innersving, og vil ved denne verdien av N(=2) ha to yttersvinger og to innersvinger tilsammen i løpet av en full rotasjon - og deres totale sporlengde rundt sentralsolen vil derfor bli identiske (for alle fire). De røde sporene tilfredsstiller også fullt ut VmLs betegnelser "et åpent sirkelløp(spiralløp)" og "spiralsirkel". På illustrasjonen kan det se ut som om yttersporet er noe lengre enn innersporet, men her må man huske på at rotasjonen foregår i 3 dimensjoner, slik at det blir ytterst komplisert å beregne den nøyaktige sporlengden. Men om det er slik at den ene modersolen i paret senker farten ørlite grann, så vil det altså være slik i helixmodellen, at nøyaktig det samme vil skje med tilsvarende modersol i det andre paret. I fremtiden vil kanskje en meget kyndig person kunne klare å beregne sporlengdene.

[3] og [5]: Aabent Cirkelløb (Spiralløb). Som man ser av ovenstående stillbilde, danner modersolparene på sin vei rundt sentralsolen et perfekt spiralløp eller sirkelløp og det er også åpent! Fordi bevegelsene foregår i tre dimensjoner, er det rom inne i spiralsirkelen - den er altså åpen innvendig, og modersolene beveger seg i et "skall" rundt det åpne sirkelformede rommet. Dette gjelder ikke for planmodellens vedkommende. Ved ekstremt høye verdier av N, kan man kanskje på en måte betrakte bevegelsen som spiralaktig, men den korrekte betegnelsen må heller være en serie med loop'er, og den sirkelen som dannes er definitivt ikke åpen - den er flat som en pannekake! Dette gjelder ved alle verdier av N, lave som høye. Det er helt flatt og har ingen åpning noen steder!

[4]: En hinanden motgående Bevegelse. Når man betrakter helixmodellens bevegelser på animasjon nr 2 ovenfor, ser man meget lett at parene har en hinanden modgående bevegelse. Men det som er meget interessant med helixmodellen, er at parene til tross for at de har denne motgående bevegelsen faktisk roterer samme vei!! Grunnen til det er at vi ser det ene paret forfra og det andre paret bakfra. Dette gjelder ikke for planmodellen, der det ene paret roterer med uret og det andre paret roterer mot uret. I verdensrommet er det slik at det kun skjer ytterst, ytterst sjelden at planeter roterer med uret. Så uansett hvordan vi betrakter modersolparene i planmodellen, så vil altså det ene paret ha en rotasjonsretning som kun opptrer i svært sjeldne tilfeller.

[6]: Men nå til det som er hovedpunktet med denne artikkelen: Avsløringen av gåten om antall rotasjoner. Det vil si, det er egentlig slett ingen gåte, fordi svaret befinner seg i VmL, dersom man bestemmer seg for å stole fullt og helt på det som står der. Det er slettes ikke første gang at man opplever å ikke finne svaret på et viktig spørsmål i VmL. I "Spørsmål og Svar" gir Leo ved flere tilfeller "mild refs" til spørsmålsstillerne fordi de ikke evner å lese svaret på sitt spørsmål ut fra teksten i VmL, fordi svaret faktisk finnes der. Slik er det også med spørsmålet om antall rotasjoner modersolparene foretar på sin vei rundt sentralsolen. Svaret befinner seg her i denne setningen:

Efter ca. 3 Millioner Aar vil Parret a-b have indtaget Parret c-d's Stilling til højre for Centralsolen og Parret c-d vice versa.

Selv har jeg lest denne setningen et stort antall ganger tidligere, men aldri helt forstått at det faktisk er her svaret ligger "skjult". For hva står det egentlig? Jo, det står at etter 3 millioner år så vil a-b ha inntatt b-c sin stilling. Og hva innebærer egentlig det? Jo, når det står beskrevet slik - uten at noe spesielt antall rotasjoner er oppgitt, kan det ikke bety annet enn at modersolparene roterer nøyaktig så mange ganger de trenger for å inntar hverandres posisjon. Det vil si: De må enten rotere en halv eller en hel gang i løpet av en halv omgang rundt sentralsolen. Roterer de en halv gang, vil parene stå slik:

c - d sentralsol b - a

Denne posisjonen vil altså bety at modersolparene har skiftet plass, men de står i omvendt rekkefølge av utgangspunktet. A og c, som startet innerst, står nå ytterst, og b og d, som startet ytterst, står nå innerst. Jeg synes dette er mangelfullt for å kunne påstå at de har inntatt hverandres stilling - de står nemlig i gal rekkefølge. Jeg vil derfor mene at for at VmLs ord skal være oppfylt, så må modrsolparene ha gjort en hel rotasjon, slik at de etter en halv runde rundt sentralsolen står slik:

d - c sentralsol a - b

Det vil jeg kalle å innta hverandres stilling! Og for å komme dit, må altså modersolparene foreta en full rotasjon. Og det vil også si at det antall ganger modersolene roterer på en runde rundt sentralsolen er: 2! Og se, det er svaret på hvor mange rotasjoner modersolparene foretar for hver runde! 2! Og jeg mener jeg tør garantere at det er det riktige svaret!

Oslo 24.11.08
Sverre Avnskog

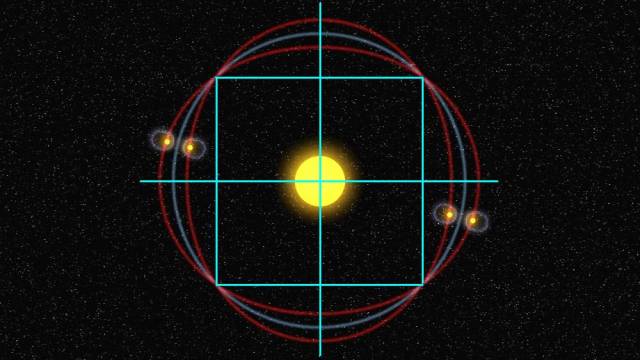For ytterligere å illustrere hvor nesten utrolig harmonisk og symmetrisk helixmodellen med 2 rotasjoner pr runde rundt sentralsolen er, har jeg satt inn noen hjelpelinjer i et stillbilde av modellen sett rett ovenfra. Kvadratet inne i storsirkelen fremkommer ved at man trekker en linje mellom alle de fire "knutepunktene" i rotasjonen - altså der hvor modersolene i hvert par står rett over og under hverandre. Det store korset fremkommer ved at man streker opp linjestykker mellom de fire posisjonene der modersolene i hvert par står rett overfor hverandre. Disse 8 posisjonene tilsammen deler opp storsirkelen i 8 nøyaktig like store sirkelbuer. Bildet av universet etter helixmodellen yttrykker en nærmest fullkommen symmetri og likevekt - presis slik Gud ville ha skapt det!!