|
Om universet for viderekommende - del 2 |
| Av Sverre Avnskog |
| Her følger enda en artikkel om universet og om modersolparenes rotasjon omkring sentralsolen. Som kjent av de fleste tilhengere av VmL, så finnes det to ulike måter å oppfatte forklaringen i VmL på - den ene tolkningsmodellen kalles gjerne for planmodellen, den andre for helix- eller propellmodellen. De som har lest mine to foregående artikler om universet vil vite at jeg er tilhenger av helixmodellen, og jeg har tidligere gjort grundig rede for hvorfor jeg mener at den må være den korrekte gjengivelsen av VmLs forklaring. På sin VmL-webside har tilhenger av planmodellen, Jørgen Degn, kommentert min artikkel, "Om universet for viderekommende", og jeg vil i det følgende presentere en analyse av hans argumenter, for om mulig å ytterligere tydeliggjøre forskjellene mellom de to modellene. Uansett hvilken modell som er den riktige, så mener jeg Jørgen overser og/eller overforenkler noen meget viktige detaljer i sin modell. Etter min mening er dette detaljer som gjør at modersolparene i planmodellen ikke fremstår med de samme harmoniske bevegelsene som i helixmodellen, der det ene parets bevegelser og hastighet til fullkommenhet speiles av det andre parets. Til opplysning: Det som gjengis i kursiv, er direkte sitater fra Jørgens artikkel - "Et univers i balanse". Til slutt i denne artikkelen vil jeg også presentere et helt nytt og meget tungtveiende språklig indisium fra en formulering i VmL, som langt på vei beviser at det er helixmodellen forfatteren av VmL har hatt i tankene da han forfattet beskrivelsen av universet. |
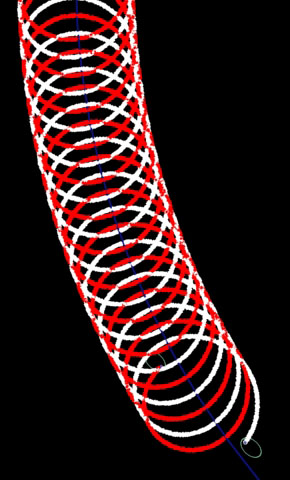
1. Falder modersolenes særbevægelse halvvejs udenfor, halvvejs indenfor storcirklens periferi?Eftersom N - antallet af parrotationer pr. 6 millioner år - endnu er ukendt, indeholder 3D-modellen mulighed for at analysere forskellige værdier af N. I mine første studier af modellen anvendte jeg lave N-værdier (bl.a. N=8) men det gik hurtigt op for mig at N formentligt antager langt større værdier. Den forskel som SA omtaler (55/45%) gør sig kun gældende ved lave N-værdier. Ved høje N-værdier (f.eks. N=50.000, se foto) elimineres denne forskel. Når N går mod uendelig går fordelingen mod 50/50% og passer fint med beskrivelsen i VML: For nogenlunde at kunne forstaa Moderklodernes Bevægelser, maa man tænke sig Universet som et Billede nedfældet paa Papiret...derved falder Modersolenes Særbevægelse halvvejs udenfor, halvvejs indenfor Storcirklens Periferi. |
 |
|
Jeg er helt enig med Jørgen i at antallet parrotasjoner(N) er en meget avgjørende faktor for hvor stor del av modersolparenes rotasjonen som vil foregå utenfor storsirkelen og hvor stor del som vil foregå innenfor i planmodellen. Den danske VmL-tilhengeren Lars Frølund Jensen har foretatt nøyaktige beregninger av den prosentvise fordelingen utenfor/innenfor storsirkelen ved en lang rekke ulike antall rotasjoner. Ved N=8 er for eksempel fordelingen 52,96/47,04 - altså en forskjell på 5,93%. Etter at Jørgen etter hvert har begynt å helle til den oppfatningen at antallet rotasjoner sannsynligvis skal være langt større, har jeg også analysert hans modell der N=50 000 for å undersøke om det er riktig det han hevder, at fordelingen går mot 50/50 når N går mot uendelig. Slik jeg ser det, har vi to ytterpunkter når det gjelder antallet rotasjoner - det laveste mulige antall rotasjoner er 1, og det høyeste mulige antall rotasjoner, er uendelig -1. Dersom vi tenker oss at antallet rotasjoner kunne være lik null (N=0), så ville planet a og c utelukkende befinne seg innenfor storsirkelen, og deres felles spor ville danne en sirkel som ligger innenfor storsirkelen med en radius lik 3 1/4 ganger sentralsolens radius. Modersolene b og d sitt felles spor ville danne en sirkel utenfor storsirkelen, med radius 3 3/4 ganger sentralsolens radius. Det sier seg selv at en meget stor andel av planetsporene ville ligge utenfor storsirkelens periferi når N=0 - fordelingen er nøyaktig 53,57/46,43, altså en forskjell på 7,14%. Dette ville være den maksimale forskjellen som ville kunne forekomme mellom rotasjonen utenfor og innenfor storsirkelens periferi. Men N kan selvfølgelig ikke være lik null, for i følge VmL skal det jo foregå et visst antall innbyrdes rotasjoner i hvert par, derfor må det laveste mulige antallet være N=1, og jeg kjenner flere VmL-tilhengere som er sikker på at dette er den faktiske verdien av N. Med N=1 vil straks situasjonen endre seg radikalt, og både plantene a og c og planetene b og d vil rotere både innenfor og utenfor storsirkelens periferi, og fordelingen vil være 53,40/46,60 - altså en noe mindre forskjell enn ved N=0. Jeg mener Jørgen Degn har helt rett når han mener at den prosentvise fordelingen utenfor/innenfor med stigende verdier av N vil bli mindre og mindre. Men vil den noensinne kunne bli 50/50? For å kunne svare på det, må vi først undersøke hva et uendelig antall rotasjoner i virkeligheten ville innebære. Altså, hva må til for at modersolparene skal kunne rotere om hverandre et uendelig antall ganger, uten noensinne å nå rundt hele storsirkelen? Jo, svaret på det er ganske enkelt at de overhode ikke kan bevege seg fremover - de må stå i ro i sin utgangsposisjon på hver sin side av sentralsolen og rotere i all evighet. Da er N=uendelig. Og hvordan ville fordelingen utenfor/innenfor storsirkelens periferi være i et slikt tenkt tilfelle - ville den være 50/50, slik Jørgen hevder i sin artikkel? Nei, det ville den ikke! På grunn av storsirkelens krumning, vil aldri fordelingen kunne bli bli 50/50! Hver modersols rotasjonsspor ville være litt lengre utenfor storsirkelen enn innenfor - i følge Lars Frølund Jensen vil den nøyaktige prosentvise fordelingen være 51,14/48,84 - en forskjell på 2,3%. At det blir en tydelig forskjell vil kunne påvises av enhver som har lyst til og interesse av det - det er bare å tegne opp sentralsolen og modersolene slik det står beskrevet i VmL, og så tegne opp de sirklene modersolparene vil danne når de roterer. Enhver vil med selvsyn kunne konstatere at en større del av buen til hver sirkel vil ligge utenfor storsirkelens periferi enn innenfor! Lars Frølund Jensens beregninger, som for øvrig er behørig presentert i en annen artikkel på websiden, bekrefter Jørgen Degns antagelse at den prosentvise forskjellen gradvis vil bli mindre med stigende verdier av N. Men den når sitt absolutte minimum dersom N=uendelig, og forskjellen er altså da 2,3%. Men fordi N ikke kan være lik uendelig, vil den situasjonen at modesolparene ikke beveger seg fremover aldri kunne oppstå. Det høyeste antallet rotasjoner modersolparene vil kunne ha, vil være N=uendelig ÷1. Lars har også beregnet forskjellen ved meget, meget høye N-verdier, og ved N=1 milliard, er forskjellen tilnærmet den samme som ved N=uendelig. Vi kan da sette opp følgende yttergrenser for N: 1 ≤ N ≤ ∞ ÷ 1 (N er større enn eller lik 1 og mindre enn eller lik uendelig minus 1), og jo nærmere 1 verdien av N befinner seg, jo større vil den prosentvise forskjellen mellom utenfor og innenfor storsirkelen være, og jo nærmere uendelig ÷ 1 verdien av N befinner seg, jo lavere vil den prosentvise forskjellen være, men fordelingen vil aldri noensinne kunne bli 50/50! Det er også svært usannsynlig at N kan anta så høye verdier som 1 000 000. Det vil i såfall innebære at hver rotasjon kun ville ta 6 år, og med de gigantiske planetstørrelsene og avstandene vi taler om her, ville det være helt absurd å tenke seg at de skulle kunne rotere rundt hverandre i løpet av så kort tid! Men overstående resonnement gjelder altså den prosentvise forskjellen! Den faktiske ulikheten i antall km i ulik lengde mellom den delen av modersolsporene som befinner seg utenfor og den delen som befinner seg innenfor storsirkelens periferi vil faktisk ikke minke, men tvert imot øke, selv om den prosentvise forskjellen blir mindre! Hvordan i all verden kan så det ha seg, vil sikkert mange undre seg? Men la oss gå tilbake til Lars Frølund Jensens beregninger som altså viser at den prosentvise ulikheten mellom sporene utenfor og innenfor storsirkelens periferi ved 50 000 rotasjoner er ca 2,3%, mens den for N=8 er ca 6%. Tar vi så i betraktning at forskjellen i den reelle strekningen modersolene tilbakelegger utenfor og innenfor er kun ca 5 ganger så lang for hver omdreining ved N=8 som ved N=50 000, skjønner man at den reelle forskjellen mellom den totale strekning modersolene tilbakelegger utenfor og innenfor sentralsirkelens periferi vil være nærmest gigantisk for N=50 000 i forhold til ved N=8. Forskjellen i reell strekning vil være nærmere 1200 ganger større ved N=50 000 enn ved N=8!!! Det blir derfor meget misvisende å påstå at forskjellen går mot null ved stigende verdier av N. Det er riktig at den prosentvise forskjellen synker, mens altså den reelle forskjellen øker. Et annet viktig aspekt, som tidligere ikke har vært ofret så mye oppmerksomhet, er at dersom man regner ut ulikheten for hvert par for seg, i stedet for å legge sammen begge sporene utenfor og begge sporene innenfor, så vil man komme frem til forskjeller som er enormt mye større. Ved N=14, er f eks gjennomsnittsforskjellen for hvert par mer enn 41%! Ved denne måten å regne ut forskjellen på, viser det seg at det er ved akkurat denne N-verdien at forskjellen er størst. Jeg antar at det må skyldes at ved N=15 begynner den ene moderolen i hvert par å bevege seg bakover i forhold til den felles fremadgående bevegelsesretningen, mens ved N=14 ser det ut til at den ene modersolen i hvert pa så og si står stille, mens den andre beveger seg hurtig forbi. Dette fenomenet kan for øvrig observeres i animasjonen av planmodellen i artikkelen "Om universet for viderekommende - del 3". |
4. Har klodernes spor samme længde?Ja, ved høje N-værdier går længden af klodesporene mod samme værdi. Ved tænkte lave N-værdier er disse klodespor parvist af forskellig længde, årsagen skyldes at rotationen sker i hver sin fase. Men intet tyder på at N antager lave værdier - tværtimod. |
|
I følge Jørgen er forskjellen mellom de parvise klodesporene ca 4 % ved N=8 - mine beregninger på basis av tall fra Lars Frølund Jensen viser en ulikhet på ca 2%. Men Jørgen har helt rett i at den prosentvise forskjellen vil bli mindre ved økende verdier for N, og dersom N kunne anta verdien uendelig, ville det bety at alle fire modersolene ville stå og rotere "på stedet hvil" uten å flytte seg fremover langs storsirkelens periferi. Da ville klodesporene være av samme lengde! Men den situasjonen vil altså aldri inntreffe i virkeligheten, og så snart N har en eller annen lavere verdi enn uendelig, så vil det øyeblikkelig oppstå en ulikhet i sporlengdene, som kommer av at det ene modersolparet roterer med uret og det andre mot uret. Det paret som roterer med uret vil ha sin "lange fremadgående bue" innenfor storsirkelen og sin "korte tilbakegående bue" utenfor storsirkelen, mens det vil være omvendt for det paret som roterer mot uret, det vil ha den "lange fremadgående buen" utenfor storsirkelen og den "korte tilbakegående buen" innenfor. Fordi alle bevegelser som foregår utenfor storsirkelen blir lengre enn de som foregår innenfor, og den fremadgående buen er lengre enn den tilbakegående, vil sporene aldri parvis kunne bli av nøyaktig lengde! Og ved N=50 000 er det fremdeles en tydelig forskjell mellom klodesporenes lengde. Men som jeg også har påvist ovenfor når det gjelder fordelingen utenfor/innenfor storsirkelens periferi, så vil den relle ulikheten mellom sporene i antall kilometer i realiteten ikke minke i samme grad som den prosentvise ulikheten blir mindre! Det fordi det store antallet rotasjoner vil medføre at modersolene skal tilbakelegge så enorme avstander, at selv en ørliten prosentvis ulikhet vil kunne bety en betydelig forskjell i reell lengde. Om vi tenker oss at modersolparene roterer med en verdi av N=1 000 000, og forskjellen mellom de parvise planetsporene kun er 1 meter i hver rotasjon, (en så minimal forskjell at den nærmest ikke vil kunne la seg uttrykke i %) så vil det likevel medføre at ulikheten etter 1 000 000 rotasjoner ville være 100 mil, som vel må sies å være en ganske betydelig forskjell tross alt! Ved N=50 000 er forskjellen i sporlengden for de to parene ca 0,002%. Dette er kanskje en meget liten prosent, men i reell ulikhet i sporlengde er forskjellen likevel så stor som ca 1/3 av ulikheten ved f. eks N=8. |
5. Er modersolenes rotationshastighed konstant?Når man diskuterer modersolenes bevægelser må man gøre sig klart om man tænker på: 1) modersolens omdrejningshastighed omkring sin egen akse (v1), 2) modersolens omdrejningshastighed omkring epicenteret (v2), 3) epicenterets omdrejningshastighed omkring centralsolens centrum (v3) eller 4) modersolens særbevægelser (v4 = v2 + v3) - den relative hastighed. I VML kan man læse: "Den engang givne Rotationshastighed for begge Parrene vil bestandig bibeholdes". "Rotationshastighed for begge par" er synonymt med parrotationshastighed eller v2, denne parameter er konstant i 3D-modellen som påkrævet. Hertil kommer at "Hver Sol har sin egen Aksebevægelse" (v1, v3) som også er konstante. Der findes ikke noget krav i VML om at v4 skal være konstant. Mine studier af planmodellen tyder på at v4 varierer på samme måde som at det fremadgående rotorblad på en helikopter har en relativ større hastighed end det tilbagegående. |
|
Her synes jeg Jørgen overforenkler et meget komplekst problem på en måte som gjør at han kommer frem til helt gale slutninger. Det virker jo besnærende dersom vi kunne regne ut hver enkelt modersols individuelle hastighet på den enkle måten han stiller opp: v4 = v2 + v3. Det er lett å falle i den fellen, men svaret blir dessverre helt galt! En overfladisk betraktning kan muligens lede noen til å mene at planetsporene i planmodellen er speilbilder av hverandre, men det er de definitivt ikke! De har parvis ulik lengde og modersolenes hastighet(v4) i sine respektive spor varierer hele tiden, uten at det finnes noen speilbildeeffekt mellom de to parenes særspor og individuelle hastighet. Og anvender man Jørgens "formel", v4 = v2 + v3, vil man jo komme frem til at dersom både v2 og v3 er konstante for begge parene, så vil automatisk også v4 bli konstant, men det er avgjort ikke tilfelle, som jeg har vist meget tydelig i min forrige artikkel - og det skyldes ganske enkelt at hans formel er gal. Det han nemlig overser, er at de to rotasjonene som modersolenes hastighet påvirkes av, ikke foregår i samme retning! Her er et eksempel som jeg håper kan illustrere mitt poeng: Tenk deg at en liten radiostyrt bil står på lasteplanet til en lastebil som kjører fremover i konstant hastighet, v2. Hvis vi tenker oss at den lille radiostyrte bilen, samtidig som lastebilen kjører rett fremover, kjører over lasteplanet på langs, med hastigheten v3, så kan man regne ut den radiostyrte bilens relle hastighet(v4) på den måten som Jørgen foreslår - den vil da bli: v4 = v2 + v3. I dette tilfellet fungerer formelen - med det er kun fordi de to hastighetene v2, og v3 har samme retning! Hvis vi tenker oss at den lille radiostyrte bilen, i stedet for å kjøre over lasteplanet på langs, startet på den ene siden av lasteplanet, og kjørte over lasteplanet på tvers med hastigheten v3, ville vi da kunne regne ut den reelle hastigheten til den lille radiostyrte bilen på samme måte? Nei, avgjort ikke, bruker vi Jørgens formel også i dette tilfelle, ville vi få til svar at den radiostyrte bilen ville ha nøyaktig samme hastighet i begge de to eksemplene, hva den selvfølgelig ikke har, fordi i det ene tilfellet kjører den i samme retning som lastebilen, og i det andre eksempelet kjører den på tvers av lastebilens kjøreretning. I eks 1 ville sporet til den lille bilen ta form av en lang rett linje, mens i eks 2 ville sporet se ut som en skråstilt linje, som ville være kortere enn den i eks 1, fordi bilen i eks 2 ikke ville bevege seg fremover på lasteplanet, men bare sidelengs, slik at man ville måtte trekke fra lasteplanets lengde fra sporet. Går vi tilbake til moderolenes bevegelser langs storsirkelen, blir det ytterligere komplisert av at modersolene faktisk hele tiden roterer omkring sirkelbuen. De beveger seg ikke kun på langs og på tvers, men faktisk i alle mulige vinkler etter hvert som de roterer. Å beregne hastigheten til hver modersol, v4, blir derfor uhyre komplisert, fordi den hele tiden vil variere, etter hvor i rotasjonen hver modersol befinner seg. Selv om selve rotasjonshastigheten, v3, hele tiden er konstant, så vil man ikke kunne legge denne sammen med v2 og så få modersolens egenhastighet, v4, til svar. Før v3 kan legges til v2, må den retningsjusteres, og det lar seg sikkert gjøre av en dyktig matematiker. Det man også kan gjøre, er å måle de avstandene hver modersol tilbakelegger i løpet av et bestemt tidsrom, og så kan man regne ut en gjennomsnittshastighet. Det som er 100% sikkert, er at fire modersoler ikke i løpet av en del av rotasjonen kan tilbakelegge fire ulike strekninger og så ha samme individuelle hastighet i forhold til et fast punkt! Det er nemlig dette som er tilfelle med planmodellen! Uansett antall rotasjoner vil ulikhetene alltid være der, om enn de vil variere med ulike verdier av N! På et gitt tidspunkt vil alle fire modersoler ha ulik individuell hastighet! |
 |
| Over ses en grafisk fremstilling av hvordan den prosentvise fordelingen mellom modersolenes spor henholdsvis utenfor og innenfor storsirkelens periferi vil endre seg ved stigende verdier av N. Ved verdien N=0, altså ingen rotasjoner, vil fordelingen være 53,57/46,43. Ved økende antall rotasjoner (økende verdier av N) vil fordelingen gå i retning av 50/50 - uten noensinne å nå dit. Dersom N kunne nå verdien uendelig, ville det bety at modersolene i praksis ville stå på stedet hvil og rotere. Ved N=50 0000 er fordelingen 51,14/48/84%. Bare ved å bruke opptil 12 desimaler i utregningene vil man kunne fastslå at den prosentvise forskjellen blir ørlite grann mindre når N stiger fra 50 000 mot uendelig. |
| Det er vanlig å operere med fire ulike hastigheter når man diskuterer universet, slik det står beskrevet i VmL. v1 angir hastigheten i hver modersols egenrotasjon, v2 er hastigheten i den "store rotasjonen" som hvert par foretar langs storsirkelen rundt sentralsolen, v3 viser hastigheten i den innbyrdes rotasjonen i hvert par og v4 er hver modersols individuelle hastighet i sitt planetspor. De som har studert min forrige artikkel, vil vite at modersolpar a-b danner en epitrochoid når de roterer med uret, mens modersolpar c-d danner en hypocycloid når de roterer mot uret. Dersom N kunne ha verdien uendelig, ville det bety at begge modersolparene ville bli stående i utgangsposisjonen og rotere i all evighet. Som det tydelig kan ses av tegningene over ville fordelingen mellom utenfor/innenfor storsirkelens periferi da være langt unna å være 50/50. Det er helt tydelig at en større del av rotasjonen ville foregå utenfor storsirkelens periferi enn innenfor. |
| Å sammenligne modersolenes rotasjonsmønster med propellbladene til et helikopter gir god mening. Men for å kunne få den fulle oversikten er det ikke tilstrekkelig å operere med kun ett helikopter, man må ha to! Og for at sammenligningen skal kunne bli reell, må propellene på de to helikopterne rotere hver sin vei, og de må kjøre i en stor sirkel. Hos helikopteret med propell som roterer med uret, vil propellbladene, når de beveger seg fremover, være på innsiden av sirkelperiferien, mens propellbladene, når de beveger seg bakover, vil befinne seg utenfor sirkelperiferien. Hos helikopteret med propell som roterer mot uret, vil det være omvendt, men rotasjonsmønsteret blir altså ikke et speilbilde! Propellbladene vil befinne seg utenfor sirkelens periferi når de beveger seg fremover, og på innsiden når de beveger seg bakover. Dette vil være analogt med universet slik det beskrives i VmL! Fordelingen utenfor/innenfor sirkelens periferi vil derfor heller aldri bli 50/50! |
| Til venstre ses Jørgens eget foto av sporene til modersolpar a-b, som roterer med uret. I følge hans opplysninger har N verdien 50 000 på dette bildet. For å kunne danne seg en sikker oppfatning av lengden av sporene, er det nødvendig å få frem kun én rotasjon og fjerne alle de øvrige. Det har jeg gjort på de to små bildene til høyre. Øverst ses den siste rotasjonen i det hvite sporet. Retningspilene er satt på av meg, for at det skal bli tydelig for leseren hvilken retning modersolen har beveget seg. Under ses den siste rotasjonen i det røde sporet, fremstilt på samme måten. |
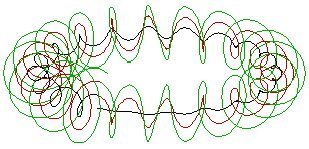
| Her har jeg gått enda et skritt videre for å illustrere lengden av sporene utenfor og innenfor storsirkelens periferi. Sporene til modersolpar a og b har jeg klippet direkte ut av Jørgens bilde og intet er forandret på lengden. Man ser tydelig at det røde sporet på utsiden av sirkelbuen krysser over den vertikale markørlinjen, mens det hvite sporet ikke når helt frem til den vertikale blå linjen. Det skyldes krummingen på storsirkelens bue. Til høyre ser man sporene til modersolpar c-d. Jeg gjør oppmerksom på at disse to er konstruert av meg fordi jeg mangler et bilde av dette paret. Men jeg har konstruert dem ved å speilvende storsirkelens bue, kopiert inn solspor a-b og forlenget/forkortet dem slik at de kommer nøyaktig frem til storsirkelens bue. Illustrasjonen gjengir likevel tydelig det som er mitt poeng, nemlig at det gule sporet er lengre enn det hvite fordi de befinner på hver sin side av sirkelbuen, det hvite innenfor og det gule utenfor. Det samme gjelder for det røde og grønne sporet, men her er forskjellen mindre fordi disse to sporene er kortere (her beveger forøvrig modersolene seg i motsatt retning). Forskjellen mellom det røde og grønne er ikke stor nok til å utligne forskjellen mellom det hvite og det gule! Den nøyaktige fordelingen utenfor/innenfor er 51,14/48,84! (Beregnet av Lars Frølund Jensen). Legg også merke til at alle de fire sporene i denne avgrensede delen av rotasjonen har ulik lengde. De skal tilbakelegges i løpet av samme tid - altså må alle fire modersolene i denne delen av sporet ha ulik individuell hastighet(v4)! Spor c-d er heller ikke et speilbilde av spor a-b! |
6. Jord-måne parretVi kan desværre ikke betragte modersolparrenes bevægelserne på afstand og dermed få bekræftiget ovenstående, men lad og i stedet se nærmere på et lignende system, nemlig jordens og månens bevægelser rundt om solen. Man bemærker nemlig at jorden og månen foretager en roterende par-bevægelse (”dans”) rundt om solen, på en lignende måde som et modersolpar roterer rundt om Centralsolen. Den eneste forskel er, at objekternes forskellige masser skrævvrider systemet, men havde månen og jorden haft samme masse, ville særbevægelserne tydeligt afspejle et modersolpars. Astrofysiker ph.d. Michael Linden-Vørnle fra Tycho Brahe Planetariet bekræftiger denne opfattelse: "Jorden og Månen roterer om deres fælles massemidtpunkt (efter vægtstangsprincippet). Hvis de havde samme masse ville dette punkt ligge lige mellem de to himmellegemer. Massemidtpunktet ville så beskrive en ellipsebane omkring Solen." |
|
Jeg har personlig meget vanskelig for å se at eksempelet med månen og jorden skulle ha noen overføringsverdi til debatten om modersolenes bevegelser omkring sentralsolen. Og jeg skal her forsøke å begrunne hvorfor. For det første så er både sola, jorden og månen mørkeplaneter, som ikke er blitt satt i deres baner i kraft av Guds vilje, men i kraft av de fysiske lover som gjelder i verdensrommet. I følge VmL er alle andre planeter i universet utslynget fra modersolene, og de tallrike planetene har funnet sine baner som en følge av tyngdekraften, tiltrekning mot større planeter osv. Dette til forskjell fra sentralsolen og modersolene, som er skapt av Gud og satt i rotasjon og fastholdt i sine baner av Guds tanke. De lovmessigheter som ligger til grunn for banene må derfor sies å være helt vesensforskjellige fra jorden og månens rotasjon rundt sola. Jeg vil derfor hevde at det ikke finnes noe grunnlag for å fremholde månens rotasjon omkring jorden som et forbilde for modersolenes rotasjon omkring sentralsolen! Sentralsolen og modersolene er dessuten lysplaneter (selv om modersolene har en kjerne av mørke, som dog er innkapslet av lyset) og det finnes vel ingen i dag som kan påstå at de kjenner til bunns i hvilket forhold disse planetene står til de hittil kjente lovene for universet. Alt fra VmL tyder på at både sentralsolen og modersolene har sin plassering og sine bevegelser som en følge av Guds vilje, og at han fastholder disse bevegelsene ved sin tanke. Her er hva som står i kommentaren i VmL om modersolenes tilblivelse: "Modersolene dannedes ved, at Gud i Kraft af sin Villie satte Æteren - Lyset og det deri bundfældede Mørke - i en roterende Bevægelse om fire Kraftcentre, der bares og fastholdtes af og i Hans Tanke. Og i dette avstittet står det med all tydelighet at det er Guds vilje som opprettholder modersolparenes rotasjon, og ikke diverse fysiske lovmessigheter: Klodernes Antal er paa hvert givet Tidspunkt begrænset - det modsatte vilde stride mod Ligevægtsloven - men i Tidernes Løb bliver Antallet ubegrænset; nye og atter nye vil bestandig fremkomme, medens ældre Kloder forsvinder, opløses i deres Bestanddele; men den samlede Vægt vil, saa længe de fire Modersolssystemer, i Kraft af Guds Villie, roterer i Verdensrummet, bestandig balancere med Nul. Saaledes bliver Klodernes Antal endeligt indenfor Begrebet Væren, men uendeligt indenfor Begrebet Vorden. Men om vi nå for et øyeblikk skulle anta at eksempelet med jorden og månen kan danne et forbilde for modersolenes rotasjon, og samtidig aksepterer at jorden og månen var av lik størrelse og vekt, slik at de ville danne en rotasjon som i planmodellen. Og om vi videre tenker oss at det fantes et identisk par til, så ville situasjonen bli helt analog med sentralsolen og de fire modersolene. Men dersom universets lovmessigheter har ført til at den, i eksempelet, like store jorden og månen roterer rundt solen i et bestemt plan og med en bestemt hastighet og retning, hvorfor i all verden skulle så et annet tilsvarende par, som en følge av nøyaktig samme lovmessigheter begynne å rotere i stikk motsatt retning av det første paret? I planmodellen roterer modersolene mot hverandre, en med uret og en mot uret. Dersom de fysiske lovmessigheter får ett par til å rotere på en bestemt måte, så måtte vel et identisk par rotere på samme måten? Eller er det slik at de fysiske lovene kan virke så forskjellig på identiske planeter i identiske situasjoner at de kan komme til å rotere stikk motsatt vei? Av ovennevnte grunner mener jeg det blir altfor enkelt å forklare at modersolene må rotere i samme plan som storsirkelen, fordi det er det mest vanlige i universet. Med tanke på at det er Gud som har skapt sentralsolen og modersolene, synes jeg det virker lite trolig at han ville skape et planetsystem med så store disharmonier, unøyaktigheter og avvikelser. Opp mot den meget unøyaktige planmodellen vil jeg personlig sette helixmodellen, der alle bevegelser, hastigheter og retningsforandringer hos det ene modersolparet til fullkommenhet speiles av det andre paret! |
 |
 |
| Disse to illustrasjonene er vel egnet til å tydeliggjøre prinsippene for modersolenes bevegelser i helixmodellen. Moderolenes spor vil danne en spiralbevegelse, der alle endringer i hastighet og rotasjonsretning hos det ene paret, vil speiles til fullkommenhet av de andre paret! I sannhet en guddommelig harmonisk bevegelse! |
7. Parallelle rotationsakserPå en forespørgsel fra min side om hvorvidt rotationsakserne i mælkevejen er parallelle svarer Michael Linden-Vørnle bekræftende at: "Det er mere reglen end undtagelsen at rotationsakser er parallelle med Mælkevejens." eller som han også forklarer med andre ord: "Da vi formoder, at planetsystemer skabes af en stor fladtrykt roterende sky af gas og støv, vil det altid være mest sandsynligt, at baneplanerne vil være mere eller mindre sammenfaldende. Ekstreme afvigelser kræver voldsomme påvirkninger - typisk i form af sammenstød. Det gør i denne sammenhæng ingen forskel om banen er en perfekt cirkel eller ej." Præcist samme forhold gør sig gældende i vort solsystem: Der kan føres et matematisk-fysisk bevis for at det forholder sig således, at alle kloderotationsakser i universet stræber mod at være parallelle. Bevisførelsen er baseret på en vurdering af det angulære moment indenfor diciplinen rotationel dynamik. |
|
I ovenstående resonnement er det vel verdt å merke seg hva som danner utgangspunktet for Jørgens hypotese, astrofysikeren Michael Linden-Vørnle's antagelse om at fordi: "planetsystemer skabes af en stor fladtrykt roterende sky af gas og støv, vil det altid være mest sandsynligt, at baneplanerne vil være mere eller mindre sammenfaldende." Fra VmL vet vi at sentralsolen og modersolene ikke er blitt til på denne måten. De er tvert imot skapt av Gud og satt i bevegelse av Gud. Selve grunnlaget for at denne antagelsen skulle gjelde for sentralsolen og modersolene faller dermed bort! Men i og med at Jørgen velger å bruke vårt eget solsystem som et eksempel på at alle rotasjonsakser i universet streber mot å være parallelle, kanskje det kunne være verdt å undersøke hvordan det forholder seg med månen, venus, merkur og de andre velkjente planetene i vårt solsystem. Og hvorfor ikke begynne med jorden - hvordan er det med jordens rotasjonsakse, er den parallell med solens? Nei, det er den ikke - den har en helningsgrad på ca 5% - og det betyr med andre ord at månen aldeles ikke roterer i samme plan som jorden roterer i omkring solen, men i et plan med en helningsgrad på 5 % i forhold til dette! Hvorfor Jørgen velger å bruke månens rotasjon rundt jorden som en viktig indikasjon på at modersolenes rotasjon rundt sentralsolen må foregå i et plan som er parallellt med storsirkelen, er meg en gåte. Om man kunne si at jord/måne-rotasjonen beviser noe så må det jo heller være at rotasjonsaksene ikke alltid er parallelle! For det samme gjelder for de fleste andre planetene i vårt solsystem også! |
|
Så til slutt skal jeg komme tilbake til det jeg lovet i innledningen - en formulering i VmL som er et meget sterkt språklig indisium på at helixmodellen må være riktig. Men er ikke alle ord og setninger snudd og vendt på for lenge siden uten at man har kunnet bevise noe som helst, vil kanskje noen spørre. Jo, mye av det som står i VmL om universet har vært diskutert frem og tilbake - uten at man har blitt enige. Men jeg vil gjerne trekke frem en formulering som ikke har vært nevnt i diskusjonene før - og etter min mening levner denne formuleringen liten tvil om at det er helixmodellen forfatteren av VmL har hatt i tankene da han forfattet sin forklaring av universet: Tænker man sig hvert af de fire Stjernesystemer som et ellipsoideformet Legeme, vil den ene Akse være = 1/7 af Radius i den aabne Cirkel (Spiralcirklen), som Moderkloderne beskriver i deres Særløb efter hinanden; den anden Akse = 1/28 af samme Spiralcirkels Buelængde, og den tredie = 3/7 af den længste Akse. Her anvendes et begrep som ikke har vært diskutert tidligere blant oss VmL-tilhengere: "den aabne Cirkel (Spiralcirklen), som Moderklodene beskriver i deres Særløb efter hinanden". Denne spiralsirkelen er selvfølgelig den sirkelformede spiral som modersolparene danner når de roterer rundt sentralsolen. For det første er det meget viktig å huske på først er ved høye verdier av N, at modersolesporene i planmodellen antar formen av noe som i det hele tatt ligner på spiraler. Men på hvilken måte kan det passe at disse helt flate modersolsporene skal kunne danne en åpen sirkel? Hvor er i såfall åpningen? I helixmodellen er det helt opplagt en åpen spiralsirkel - spiralen vil være åpen i hele rommet gjennom sirkelen, mens planetsporene vil ligge som spiraler i "skallet" til den åpne sirkelen. For meg personlig gjelder den ovenstående formuleringen, i tillegg til alle de andre unøyaktigheter som hefter ved planmodellen, som et ugjendrivelig bevis for at det kun er helixmodellen som tilfredsstiller VmLs forklaring. Andre vil selvfølgelig være av en annen oppfatning, men jeg håper i hvert fall at mine artikler om universet kan være med på å tydeliggjøre hva uenigheten vedrørende planmodellen og helixmodellen går ut på! Helt til slutt vil jeg råde Jørgen til å kontakte en språkekspert, slik at han ikke fortsetter å tro at det som står i VmL om at man for nogenlunde å forstå forklaringen av universet, bør nedfelle det som en tegning på papiret, betyr hvarken at forklaringen i VmL bare er sånn nogenlunde korrekt, eller at den modellen som lettest lar seg tegne på papir, er den som er mest korrekt! Den omtalte setningen betyr ganske enkelt at man oppfordres til å tegne en skisse av universet for lettere å forstå forklaringen! Det er spennende å diskutere forskjellige oppfatninger av VmL, men man bør sikre seg at ens språklige oppfatninger samsvarer med gjeldende språkregler. |
 |
 |
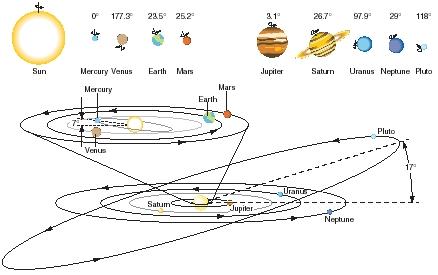
| Illustrasjonen til venstre viser planetenes rotasjonsplan rundt solen, og deres respektive rotasjonsaksers avvikelse fra å være parallelle med solens. Som man ser så er det kun Merkur som har en rotasjonsakse som er parallell med solens. De andre avviker med fra 3,1(Jupiter) til 177,3 grader(Venus). Som man ser har Merkur og Pluto rotasjonsplan som avviker fra de andre planetenes. Merkurs rotasjonsplan får sågar øket vinkel i forhold til de andre planetenes rotasjonsplan for hver eneste rotasjon planeten gjør rundt solen. |
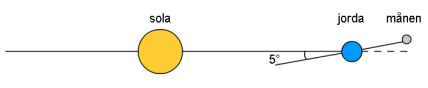
| Jørgen velger i sin artikkel å bruke månens rotasjon rundt jorden som et indisium på at planmodellen må være den som best tilfredsstille de fysiske lovmessigheter. Det til tross for at månen aldeles ikke roterer rundt jorden i samme plan som jorden roterer rundt sola, men i et plan med en helningscinkel på ca 5 grader. Det er vanskelig å se dette som et bevis på planmodellens riktighet, vil jeg påstå! (Illustrasjon fra Universitetet i Oslo) |
|
I vårt solsystem er det kun Merkur som har rotasjonsakse som er parallell med solens, men den har på den annen side en meget ustabil rotasjon, og roterer i et plan som stadig endrer seg for hver omdreining. Verdt å merke seg er også Pluto, hvis rotasjonsplan avviker med ca 17 grader fra de andres. Men bortsett fra dette, så har altså samtlige andre planeter rotasjonsakser som avviker fra Solens - og dette innebærer at ingen av deres mange måner roterer i samme plan som dem selv. Ellers roterer også alle mot uret, unntatt Venus, som har en retrograd bevegelse i sin egenrotasjon. Saturn, som har opptil 60 måner (antallet varierer fra kilde til kilde) er den eneste planeten som har en måne som roterer med uret, det er månen som heter Phoebe, ellers roterer alle planeter og måner i vårt solsystem mot uret! Om vi kan trekke noen konklusjoner om hva som er vanlig i universet utfra å studere vårt eget solsystem, må det bli dette: - Det er høyst uvanlig at planetene har parallelle rotasjonsakser. I vårt solsystem er det kun én planet som har parallell rotasjonsakse med solen, de andre avviker med fra 3,1 til 177,3 grader! Jorden har et avvik på 5 %. - Det er høyst uvanlig at planeter i universet roterer med uret. På fagspråket kalles denne typen rotasjon for en "retrograd bevegelse". I vårt solsystem forekommer det kun ved 2 tilfelle, Venus og en av Saturns 60 måner. Skulle vi bruke solsystemet som et sannhetsbevis angående modersolene, kunne vi altså påstå at det det strider mot all lovmessighet at det ene modersolparet roterer med uret! La meg forresten legge til at det er kun i planmodellen at modersolparene roterer hver sin veg - det ene med uret og det andre mot uret. Når det i forklaringen i VmL står at modersolene har en hinanden motgående bevegelse, så kan jo dette virke som en meget tungvint måte å si at de roterer hver sin vei - men dersom helixmodellen er riktig, blir dette den eneste måten å uttrykke at de har en motsattrettet bevegelse, uten dermed å si at de roterer hver sin vei, og i mine øyne bekrefter denne formuleringen at det er mest sannsynlig at helixmodellen må være riktig! Når modersolene i helixmodellen har en hinanden motgående bevegelse, så betyr nemlig ikke det at de roterer hver sin vei - det betyr kun at de roterer mot hverandre når de står i opposisjon til hverandre på hver sin side av sentralsolen. Men fordi deres rotasjonsplan står vinkelrett på sentralsolen, så betyr det at i denne posisjonen så ser vi det ene paret forfra og det andre paret bakfra. Dersom det ene paret for en stund sto stille, slik at det ble tatt igjen av det andre og de sto og roterte helt inntil hverandre, ville man se at de roterer hver sin vei. Slik blir det ikke i planmodellen der parene roterer i samme plan som storsirkelen. Her rotererer parene motsatt vei hele veien rundt storsirkelen, det ene med uret og det andre mot uret. I vårt solsystem skjer det altså uhyre sjelden at planeter roterer med uret, slik det ene paret gjør i planmodellen! Jeg tror jeg må konkludere med at et studium av det solsystemet vi er en del av, ikke akkurat bekrefter sannsynligheten at de fysiske lovmessigheter i universet automatisk må føre til at planmodellen må være riktig! Jeg vil heller si tvert imot! |
 |
 |
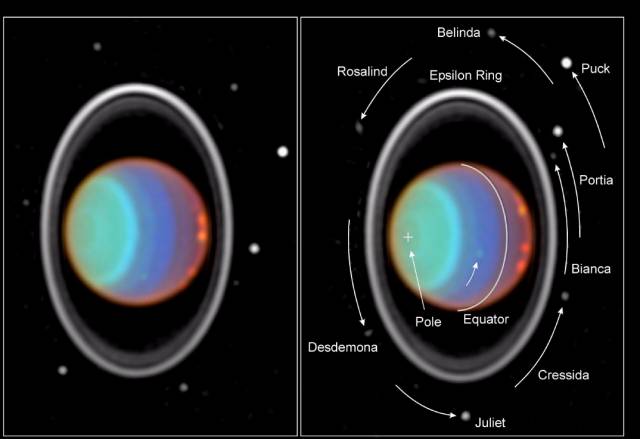 |
| Uranus er kanskje det tydeligste eksempelet i vårt solsystem på mangfoldet av rotasjonsformer. Uranus' rotasjonsakse står nesten vinkelrett på solens (97,9 grader), og til venstre ses et fotografi av Uranus og en del av månene som roterer rundt planeten. På bildet til høyre er navnet på månene satt på, og også små piler som viser deres rotasjonsretning. Som man ser, vil deres rotasjonsspor danne noe som minner om "hjul" som roterer vinkelrett på solens rotasjonsakse! I det hele tatt er det ikke mye ved planetene i vårt solsystem som bekrefter at planmodellen må være riktig, etter min mening! |
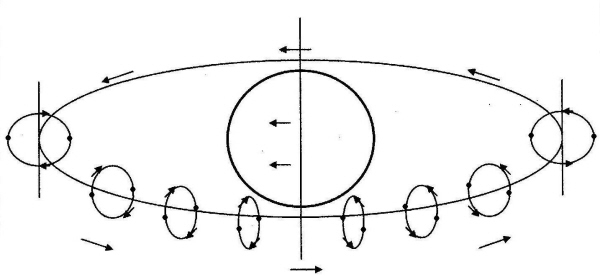
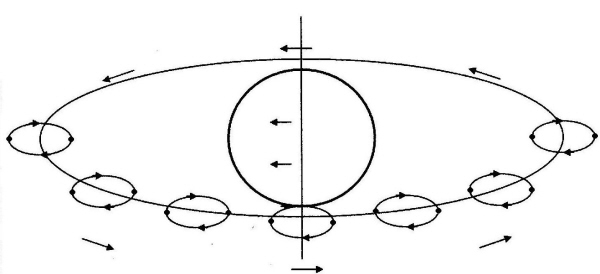
| I vårt solsystem er det uhyre sjelden at planeter roterer med uret, enten i sin egenrotasjon, eller i sin rotasjon omkring en annen planet. Det ikke mange tenker over, er at i helixmodellen roterer i realiteten modersolparene samme vei! Det er kun fordi det ene paret betraktes forfra på veg mot oss, og det andre paret bakfra på vei fra oss, at man kan si at de har en motsattrettet rotasjonsretning. På illustrasjonen øverst kan man følge et av modersolparene i flere stillbilder mens det roterer mot den motsatte posisjon, på den andre siden av sentralsolen. Som man ser, inntar modersolparet det andre parets utgangsposisjon hva angår rotasjonsretning. Det er ikke tilfellet i planmodellen, slik det fremgår av den nederste illustrasjonen. Jeg har tegnet inn modersolpar a-b, som også kan følges i flere posisjoner frem til det faller sammen med par c-d's posisjon. Som man ser, roterer modersolpar a-b fremdeles med uret, når det har nådd c-d's utgangsstilling. Det betyr at det ene paret roterer med uret og det andre paret mot uret. Mens altså i helixmodellen roterer begge parene samme vei, og om man velger å si at de roterer med eller mot uret, kommer an på hvilken posisjon de betraktes fra. (Proposjonene er ikke helt korrekte på disse tegningene!) |
|
Oppsummering: 1. Selv om det er riktig at den prosentvise fordelingen mellom modersolenes rotasjon utenfor/innenfor storsirkelens periferi blir stadig lavere ved stigende antall rotasjoner, vil fordelingen aldri kunne bli 50/50 i planmodellen! Selv ved verdien N=50 000 er forskjellen fremdeles 2,3%. I helixmodellen vil fordelingen alltid være nøyaktig 50/50 uansett antall rotasjoner. 2. Selv om den prosentvise forskjellen blir mindre ved stigende N-verdier, blir ikke den relle forskjellen mindre i samme grad. 1% utgjør en langt større reell forskjell ved høye verdier av N (f.eks 50 000) enn ved lave verdier (f.eks 1). Dette problemet vil aldri oppstå i helixmodellen! 3. Selv om forskjellen mellom de parvise sporene blir mindre ved økende verdier av N, vil de aldri kunne bli nøyaktig like lange! Dette skyldes at modersolparet som roterer med uret, vil ha en større av sitt spor innenfor storsirkelens perifer, og en mindre del utenfor, og paret som roterer mot uret, vil ha en større del av sitt spor utenfor storsirkelens periferi, og en mindre del innenfor. Forskjellene kan aldri kunne utlignes 100%! Så lenge modersolparene beveger seg fremover vil det alltid være en viss forskjell! Og det samme vil gjøre seg gjeldende her som ved fordelingen utenfor/innenfor storsirkelens periferi. Selv om den prosentvise forskjellen mellom sporenes lengde blir mindre ved økende verdier av N, vil den reelle forskjellen ikke minke i samme grad. En forskjell på 1 meter pr rotasjon, vil f. eks ved 1 000 000 rotasjoner bety en samlet forskjell mellom de parvise sporene på 100 mil! I helixmodellen vil det ene parets planetspor ha nøyaktig samme lengde som det andre uansett antall rotasjoner! 4. Jørgen mener han kan regne ut modersolenes individuelle hastighet i sitt spor ved hjelp av formelen v4 = v2 + v3, og kan på den måten komme frem til at de modersolene alltid har stabil og lik hastighet (v4). Dette er helt galt! For å kunne legge sammen hastigheter på den måte, må planetene hele tiden bevege seg i samme retning - både i den "store" rotasjonen omkring sentralsolen og i den "lille" rotasjonen omkring hverandre! Det gjør de så definitivt ikke! En mye bedre måte å sammenligne solenes individuelle hastighet på, er å måle sporenes lengde i avgrensede deler og sammenligne lengden de skal tilbakelegge i løpet av samme tidsrom. Slike beregninger viser at modersolparene hele tiden akselerere og avtar i hastighet gjennom hele rotasjonen! På gitte tidspunkt vil alle fire modersoler ha ulik hastighet. Dette i kontrast til helixmodellen, der alle hastigheter og bevegelser hos det ene paret alltid speiles av det andre paret. 5. Jørgen anvender månens rotasjon rundt jorden som et eksempel som skal sannsynliggjøre at planmodellen er den riktige. Problemet som knytter seg til denne sammeligningen er at jordens rotasjonsakse aldeles ikke er parallell med solens! (Avvik 5%). Det samme gjelder for alle planetene i vårt solsystem - unntatt Merkur. Helningsgraden for planetenes rotasjonsakse i forhold til solens er fra 3 til 177 grader. Dette i kontrast til Jørgens påstand om at alle rotasjonsakser i universet tenderer mot å være parallelle. Det finnes også ytterst få eksemplet på at planeter i vårt solsystem roterer med uret, slik som det ene modersolparet gjør i planmodellen! I helixmodellen roterer i realiteten begge parene samme vei, og har derfor en motsattrettet rotasjonsbevegelse i sin posisjon på hver side av sentralsolen. 6. I forklaringen i VmL brukes flere ganger uttrykket modersolparenes "felles bane"! I planmodellen har ikke modersolparene en slik felles bane. De to parene danner hvert sitt sett med tydelig forskjellige baner. Der hvor de to modersolparene begge har beveget seg etter hverandre, vil det tegne seg fire spor - to for hver modersol!( Selv om de to og to er like, men forskjøvet i forhold til hverandre) I helixmodellen har de to parene en fullkomment identisk bane rundt sentralsolen. Når hvert par har rotert halve veien rundt sentralsolen og befinner seg i det andre parets utgangsposisjon, vil hver modersol med 100% nøyaktighet gli inn i den forutgående modersols bane! Man kan med rette anvende uttrykket "felles bane"! |
 |
| For å illustrere helixmodellen, kan man anvende to helt vanlige propellfly, med propeller som roterer samme vei. De må kjøre i en stor sirkel, hvert fly på hver sin side av sentrum i sirkelen. Propellbladene ville befinne seg nøyaktig 50% utenfor og 50% innenfor sirkelens periferi. Propellens bevegelsesmønster hos det ene flyet vil bli et fullkomment speilbilde av det andres. Dette i motsetning til planmodellen, som kan vises ved hjelp av to helikoptre - men ikke to vanlige helikoptre - de må ha propeller som roterte hver sin vei. Propellenes bevegelsesmønster vil være tydelig forskjellig og propellbladene vil aldri kunne befinne seg nøyaktig 50% utenfor og 50% innenfor sirkelens periferi. |
|
Oslo, 30.07.08 |
 |
| Slik omtrent vil et av sporene se ut i helixmodellen. Hvis man roterer spiralen en halv "sløyfe", vil den vise også det andre sporet. I den spiralsirkelen de to identiske spiralene danner, vil begge modersolparene bevege seg i samme bane. Jeg vil også mene at betegnelsen, åpen sirkel passer mye bedre på denne 3-dimensjonale spiralsirkelen enn de helt flate spiralsirklene i planmodellen. (Det er undertegnedes fingre som synes såvidt, idet jeg holder endene på en kulepennspiral fast! Foto: Sverre Avnskog |
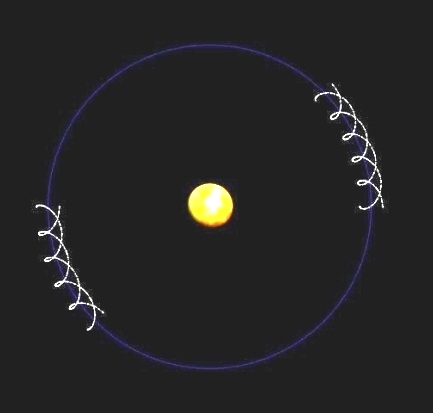 |
| Dette bildet av planmodellen viser at det egentlig vil danne seg to ulike "spiraler" i planmodellen, en for det paret som roterer med uret, og en annen for det paret som roterer mot uret. Jeg vet ikke med sikkerhet hva verdien av N er på dette bildet, men man ser i hvert fall at hvert planetspor har fått en liten tilbakegående sløyfe. Når sporene til hvert par når halvveis rundt vil man se tydelig at det tegner seg fire spor, mens det i helixmodellen kun vil være to spor! Og hvordan i all verden kan man hevde at den sirkelen de fire sporene danner er åpen? For meg fortoner den seg som helt flat og lukket! Den er jo riktignok åpen i midten, men det er jo alle sirkler! Det er helt usannsynlig at det er det ordet "åpen" henviser til. Foto: Jørgen Degn |
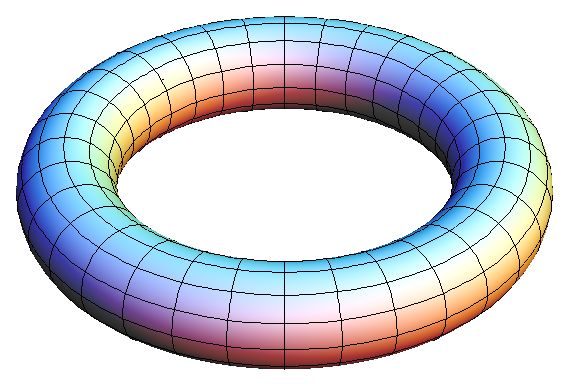 |
| Denne illustrasjonen av hva som kalles en "torus", synes jeg kan forklare meget fint hva som menes med "en åpen sirkel (spiralsirkel)" i VmL. Hvis man tenker seg at rummet inne i figuren er helt åpent, og at modersolsporene ligger som 3-dimensjonale spiraler i "skallet" til figuren, så får man et bilde som fullt ut tilfredsstiller betegnelsen en åpen sirkel (spiralsirkel). Jeg kan ikke med min beste vilje se hvordan de flate sporene i planmodellen på noen som helst måte kan betraktes som en "åpen sirkel". |